| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
 | |  |
|
Занятие №2
|
| 02.12.2012, 12:29 |
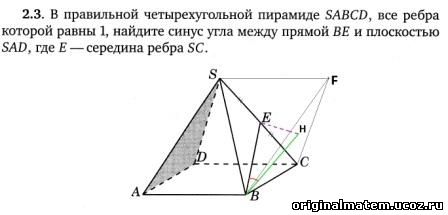
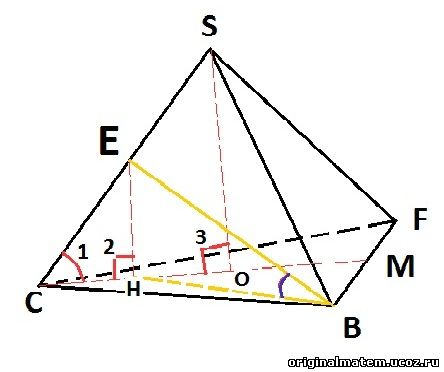Решение.
1.
Построим SF║AB, SF=AB.
2.
(ASD) ║(BFC), т.к. AS║BF, AD║BC, AB∩BF=B.
3.
Построим EH┴(BFC).
4.
5.
SO┴(CBF), O принадлежит CM , EH┴(CBF), следовательно, SO║CH, значит, Н принадлежит СМ.
6.
∆ECH ~∆SCO (∟1-общий, ∟2=∟3), SC/EC=2/1=k,EH=1/2 SO.
7. Найдем SO. ∆SCO,
CO=2/3 CM,
CM=√CF2-MF2=√1-1/4=√3/2, значит, CO=2/3∙√3/2=√3/3. SC=1, CO=√3/3, SO=√1-(√3/3)2=√2/√3.
EH=1/2SO=√6/6.
8.
Вернемся к
исходному чертежу. EH┴(CBF), BH проекция, ВЕ наклонная, следовательно, ∟ЕВН= ∟(ВЕ)(ВСF)=
∟(BE)(ADS).
9. Найдем ВЕ из ∆BES BE=√1-1/4=√3/2, sin∟HBE=HE/BE=√6/6: √3/2=√2/3.
Примечание
корень квадратный относится ко всей разности, а в ответах только к числителю.
Если корень присутствует в числителе и в знаменателе, то так это и написано.
|
|
Категория: Заочная математическая школа | Добавил: Ласточка
|
| Просмотров: 424 | Загрузок: 0
| Рейтинг: 0.0/0 |
| |
 | |  |
|
|
