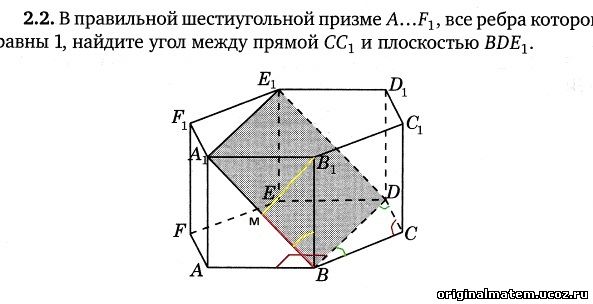
Решение. 1.     ВВ1║СС1, значит, можно рассмотреть угол между прямой ВВ1 и плоскостью ВDЕ1. 2.     Докажем, что ВD┴ (ABB1). 1) ∆DCB равнобедренный, ∟С=120, ∟D=∟B=30. 2) ∟ABC=120, ∟ABD=120-30=90, значит, DB┴AB. 3)BB1┴(ABC), т.е. BB1┴ ВD, ВD┴ BB1. 4)  ВD перпендикулярен BB1 и AB, значит, ВD┴ (ABB1). 3.     Построим перпендикуляр к плоскости BDE1 из точки В1. Для этого поступим следующим образом: построим В1М ┴А1В (М середина А1В, т.к. ∆А1В1В равнобедренный). ВD┴ (ABB1), следовательно, ВD┴ B1М. Итак, В1М ┴А1В и B1М┴ ВD, следовательно, B1М┴ (ВDЕ1). 4.     B1М┴ (ВDЕ1), B1В наклонная, ВМ проекция. Следовательно,                                            ∟В1ВМ=∟(ВВ1)( ВDЕ1).      5.  ∟ В1ВМ=45.